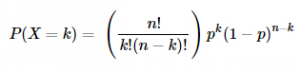R is considered as the de facto programming language for statistical analysis right? But In this post, I will show you how easy it is to implement statistical concepts in Python. I will implement discrete and continuous probability distributions in Python. I wont be getting into the mathematical details of these distributions, but I will link you to some of the best resources to learn these statistical concepts. Before getting into these probability distributions, I want to give a glimpse of what a random variable is. A random variable quantifies the outcomes of a number.
For example, a random variable for a coin flip can be represented as
X = { 1 heads
2 if tails}
A random variable is a variable that takes on a set of possible values (discrete or continuous) and is subject to randomness. Each possible value the random variable can take on is associated with a probability. The possible values the random variable can take on and the associated probabilities is known as probability distribution.
I encourage you to go through scipy.stats module.
There are two types of probability distributions, discrete and continuous probability distributions.
Discrete probability distributions are also called as probability mass functions. Some examples of discrete probability distributions are Bernoulli distribution, Binomial distribution, Poisson distribution and Geometric distribution.
Continuous probability distributions also known as probability density functions, they are functions that take on continuous values (e.g. values on the real line). Examples include the normal distribution, the exponential distribution and the beta distribution.
To understand more about discrete and continuous random variables, watch Khan academies probability distribution videos.
Binomial Distribution
A random variable X that has a binomial distribution represents the number of successes in a sequence of n independent yes/no trials, each of which yields success with probability p.
E(X) = np, Var(X) = np(1−p)
If you want to know how each function works, you can use help file command in your I python notebook. E(X) is the expected value or mean of the distribution.
Type stats.binom? to know about binom function.
Example of binomial distribution: What is the probability of getting 2 heads out of 10 flips of a fair coin?
In this experiment the probability of getting a head is 0.3, this means that on an average you can expect 3 coin flips to be heads. I define all the possible values the coin flip can take, k = np.arange(0,11), you can observe zero head, one head all the way upto ten heads. I am using stats.binom.pmf to calculate the probability mass function for each observation. It returns a list of 11 elements, these elements represent the probability associated with each observation.


You can simulate a binomial random variable using .rvs. The parameter size specifies how many simulations you want to do. I ask Python to return 10000 binomial random variables with parameters n and p. I am printing the mean and standard deviation of these 10000 random variables. Then I am going to plot the histogram of all the random variables that I simulated.


Poisson Distribution
A random variable X that has a Poisson distribution represents the number of events occurring in a fixed time interval with a rate parameters λ. λ tells you the rate at which the number of events occur. The average and variance is λ.

E(X) = λ, Var(X) = λ
Example of Poisson: what is probability of observing 4 accidents at an intersections in a day given the rate of accidents is 2 per day?
Lets consider on an average 2 accidents occur per day. Implementing Poisson distribution is more or less similar to binomial distribution, but in Poisson distribution the rate parameter is specified. The output of Poisson distribution is an array that consists of probability of 0 accidents happening, probability of 1 accident happening, probability of 2 accidents happening….up to ten accidents. Then I generate a plot



You can notice that the number of accidents peaks around the mean. On an average you can expect lambda number of events. Try different values of lambda and n, then see how shape of the distribution changes.
Now I am going to simulate 1000 random variables from a Poisson distribution.


Normal Distribution
The normal distribution is a continuous distribution or a function that can take on values anywhere on the real line. The normal distribution is parameterized by two parameters: the mean of the distribution μ and the variance σ2.

E(X) = μ, Var(X) = σ2


Normal distribution can take values from minus infinity to plus infinity. You can notice that I am using stats.norm.pdf as normal distribution is a probability density function.
Beta Distribution
The beta distribution is a continuous distribution which can take values between 0 and 1. This distribution is parameterized by two shape parameters α and β.

The shape of beta distribution depends on the values of alpha and beta values. Beta distribution is predominantly used in Bayesian analysis.


When you set alpha and beta equal to one, then the distribution is called an uniform distribution. Experiment with different alpha and beta values, and see how shape of the distribution changes.
Exponential Distribution
The exponential distribution represents a process in which events occur continuously and independently at a constant average rate.
![]()
![]()
I set the lambda parameter as 0.5 and x in the range of


Then I simulate 1000 random variables from an exponential distribution. scale is the inverse of lambda parameter. ddof in np.std is equal to dividing the standard deviation by n-1.


Conclusion
Distributions are like blue print for building a house, and random variable is summary of what happen in a experiment. I would recommend you to watch the lecture from harvard data science course, professor Joe Blitzstein gives a summary of everything you need to know about statistical models and distributions.
About Author- Manu Jeevan writes about digital analytics, data science and growth hacking. His love for data science and analytics started when he was doing his MBA. To sharpen his digital analytics and data analysis skills, he took special interest in subjects like business analytics, market research and statistics. Currently he spends all of his time on Big-data-examiner.com, his number one goal is to share what he had learned with others.